In SPM, a parametric modulation regressor is used to predict variability in the strength (that is, height/amplitude) of the neural response across different instances of the same condition. To construct such a regressor, we first need to construct a regressor that represents the mean or time-invariant neural response to the condition:
nTR = 100; % number of TRs
onsets = [5 25 45 65 85]; % trial onsets (in TRs)
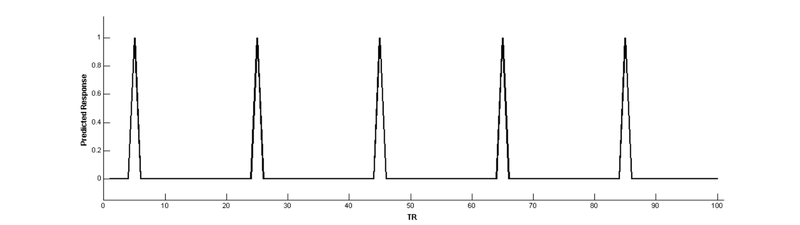
ME = zeros(nTR,1); % creates a vector of 100 TRs (all zeros for now)
ME(onsets) = 1; % puts 1s where trial onsets occu
Note that the height of the predicted response doesn’t change over time:
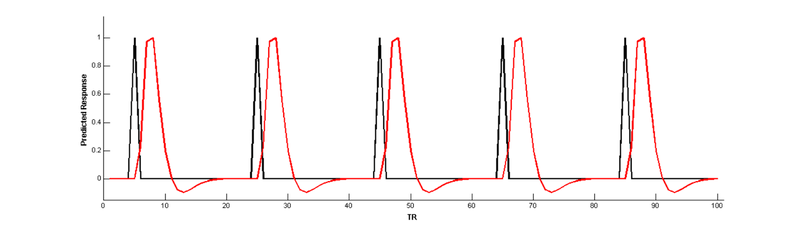
Convolve with a hemodynamic response function (HRF) to make a BOLD prediction:
bf = spm_hrf(2); % define the basis function
cME = conv(bf,ME); % convolve main effect with basis function
cME = cME(1:nTR); % remove extra values added by convolution
cME = cME/max(cME); % scale to a max of 1 (for visual comparison)
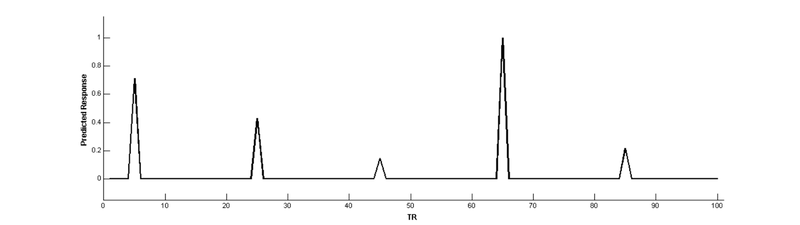
Now, use a parameter to create a new regressor that modulates the height of the main effect regressor
parameter = [5 3 1 7 1.5]; % the parameter (size corresponds to onsets)
PM = zeros(nTR,1); % creates a vector of 100 TRs (all zeros for now)
PM(onsets) = parameter/max(parameter); % puts same scale as main effect
Convolve with the HRF:
cPM = conv(bf,PM); % convolve with HRF
cPM = cPM(1:100); % remove extra values added by convolution
cPM = cPM/max(cPM); % scale to a max of 1 (for visual comparison)
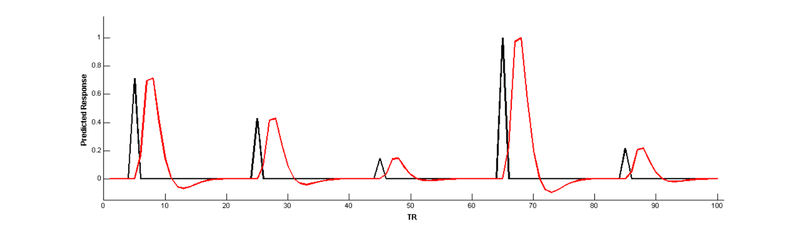
But wait, there’s a problem here! The parametric modulation regressor is highly correlated with the main effect regressor:
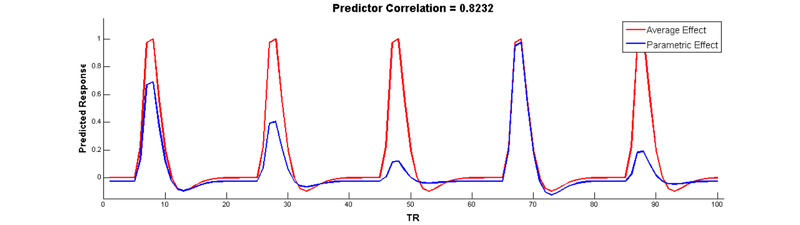
Collinear regressors like these are extremely problematic for estimating regression models. Fortunately, we can eliminate this correlation by orthogonalizing the parameter _before_modulating the height of the main effect. The easiest way to do this is to simply de-mean the parameter, i.e., subtract out the mean from every value so that it is centered around 0:
oparameter = parameter - mean(parameter); % de-mean the parameter
oPM = zeros(nTR, 1); % another vector of zeros
oPM(onsets) = oparameter/max(oparameter); % re-scale
coPM = conv(bf,oPM); % convolve
coPM = coPM(1:100); % remove extra values
coPM = coPM/max(coPM); % re-scale
Wow, no more correlation! Check it out:
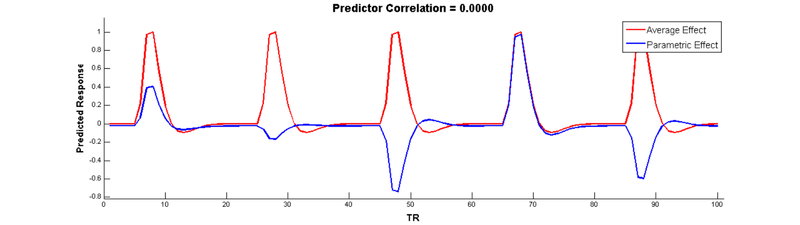
In SPM, parametric modulators are automatically orthongalized by default, so you don’t have to manually de-mean them yourself. However, note that when your have more than 1 parametric modulator specified for a given condition, SPM uses what is called serial orthogonalisationto orthogonalise the parameters. There is a good explanation of orthogonalization in SPM on theMRC-CBU Wiki.